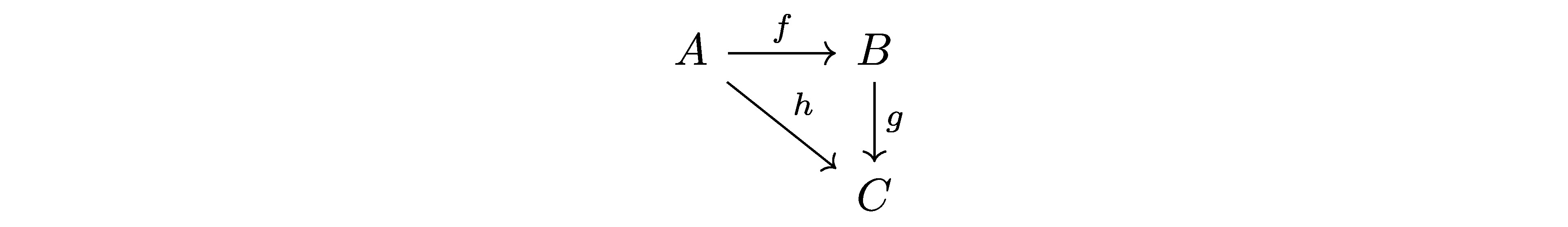推导Simply Typed Lambda Calculus的范畴论语义

本文需要读者对Simply Typed Lambda Calculus（下称STLC）有基本的了解。本文不需要读者对范畴论有任何了解————当然已经有些基本概念是极好的。本文的目标是通过推导得出STLC的范畴论语义中的构造： Cartesian Closed Category————虽然本来我是这么打算的，并且最终也这么做了，但我写着写着，就变成了“从STLC出发理解与推导范畴论基础”。这就是说，本文不仅会从STLC出发推导出它的范畴语义；在此之前，它还会把必要的全套范畴基本构造，例如product和terminal object，从STLC出发推导出其定义。这使得文章变得比我想象中长了。但我认为这种推导非常有意思，希望你看得过瘾。

老生常谈的范畴论五分钟速成

其实STLC的范畴论语义需要用到的范畴论真的不多。所以，在这里拉出一些篇幅来做范畴论速成也是可能的。不过，即使是五分钟范畴论速成，我也想要贯彻本文的宗旨：尽量推导而不是呈现各种构造。

在定义什么是一个范畴之前，我们要知道为什么我们需要一个这样的定义，范畴可以用来刻画什么数学结构的性质————这正是范畴论与抽象代数和意义：我们把各种数学构造内部共通的结构找出来，通过对这些结构的研究，我们就可以对各种数学构造有更根本的认识。所以尽管这会使得文本变长，我将从简单的抽象代数出发给出范畴的构造。已经了解范畴论的读者可以放心跳过这一节。当然，你也可以花上一分钟看看我心目中范畴这一概念应当如何引入。

让我们首先考虑两个非常具体的数学构造：实数上的加法与实数上的乘法。首先，容易观察到这两个操作对于各自的集合都是封闭的：如果$a, b \in \mathbb{R}$, 那么$a + b \in \mathbb{R}$；如果$a, b \in \mathbb{R}$，那么$a \times b \in \mathbb{R}$。此外，这两种操作无疑都满足结合律：$a + (b + c) = (a + b) + c$，$a \times (b \times c) = (a \times b) \times c$。最后，观察到对于这两个操作，都有一个具有特别意义的元素： \[ \begin{aligned} \forall a \in \mathbb{R}, \quad a + 0 = 0 + a = a \\ \forall a \in \mathbb{R}, \quad a \times 1 = 1 \times a = a \end{aligned} \] 所以尽管加法与乘法无疑是两个不同的操作，当应用在合适的集合上时，它们具有相同的结构。所以我们可以把这一结构抽象出来研究。在上面的两个例子中，我们研究的都是一个集合，记作$M$，以及$M$上的一个二元操作，记作“$\cdot$”。如果我们用$(M, \cdot)$来描述上面找到的共同结构： \[ \begin{aligned} \forall a,b \in M, \quad &a \cdot b \in M \\ \forall a,b,c \in M, \quad &a \cdot (b \cdot c) = (a \cdot b) \cdot c \\ \exists e \in M, \forall a \in M, \quad &a \cdot e = e \cdot a = a \end{aligned} \] 其中$e$被称为单位元。满足这三条性质的一个$(M, \cdot)$的组合，就是一个幺半群。如果我们抽象地证明了幺半群具有某种性质，那么实数加法、实数乘法以及其他所有具有相同结构的数学构造都免费得到了同样的性质。这就是为什么我们需要抽象代数、需要范畴论。

你也许已经观察到了，加法与乘法还具有一条额外的性质：它们是满足交换律的。 $a + b = b + a$，$a \times b = b \times a$。所以我们可以加上这条性质，得到一种新的数学结构、并研究它的性质。但加入更多限制也意味着某个数学结构能刻画的具体对象会减少。例如，如果加上交换律，我们就不能刻画从一个集合到它自身的所有函数了：从一个集合$S$到它自身的所有函数、加上函数的复合“$\circ$”，同样是一个幺半群： \[ \begin{aligned} \forall f, g : S \rightarrow S, \quad &(f \circ g) : S \rightarrow S \\ \forall f,g,h : S \rightarrow S, \quad &f \circ (g \circ h) = (f \circ g) \circ h \\ \forall f : S \rightarrow S, \quad &\text{id}_S \circ f = f \circ \text{id}_S = f \\ &(\forall s \in S, \text{id}_S(s) = s) \end{aligned} \] 抽象代数的强大，很大程度上在于它可以刻画的对象的范围是无所不含的，绝不会仅仅局限于数字。函数与数字这样看似毫无关联的对象，也可以具有高度相似的结构。

接下来，一个很自然的问题是：我们要如何刻画从一个集合到另一个集合的函数呢？很显然，幺半群的抽象并不能达成这一目的：如果$f,g : A \rightarrow B$而$A$、$B$是不同的集合，这两个函数根本就不能复合。所以我们需要一种新的抽象。如果直接以集合上的函数为蓝本，我们可以给出这样的一个定义：

我们需要一些对象$A, B, C, ...$
对象间有一些箭头$f, g, ...$，每个箭头都有一个源和一个目的地。我们可以用$f : A \rightarrow B$来表达一个箭头$f$的源和目的地。
如果$f : A \rightarrow B$，$g : B \rightarrow C$，那么$g \circ f : A \rightarrow C$也是一个箭头（幺半群的封闭性的加强版）
箭头的复合满足结合律
对于每一个对象$A$，存在一个特殊的箭头$\text{id}_A$，对于所有$f : A \rightarrow B$与$g : C \rightarrow A$， $f \circ \text{id}_A = f$，$\text{id}_A \circ g = g$ （幺半群中单位元存在的加强版）

这样我们就得到了一个“多点”的幺半群加强版。这个数学结构可以用来刻画集合间的函数，以及很多其他东西。这个数学结构有个帅气的名字，叫范畴。我们通过$A, B \in \mathcal{C}$来表达$A$、$B$是$\mathcal{C}$中的对象，通过$f \in \mathcal{C}(A, B)$来表达$f$是$\mathcal{C}$中从$A$指向$B$的箭头。

我们说范畴可以看成一个“多点”的幺半群。那么，反过来，一个幺半群就是一个只有一个对象的范畴。代入上面范畴的定义我们可以很容易地验证这一点。因此，实数加法和实数乘法也可以用范畴来刻画：这个范畴中只有一个对象，这个对象是什么都可以。这个范畴中的箭头是实数，箭头的复合则是加法（乘法），单位箭头就是0（1）。所以，箭头何须是一个直觉上的“箭头”，复合又何须是直觉上的“首尾相连”？重要的是背后的结构，而不是具体的数学对象。

最后，我们还需要了解范畴论中十分常用的工具：交换图。交换图就是把范畴中我们关心的一些箭头用图的形式画出来。交换图中，两个顶点间的所有箭头，包括通过复合隐式地产生的，都必须相等。例如，在下面的交换图中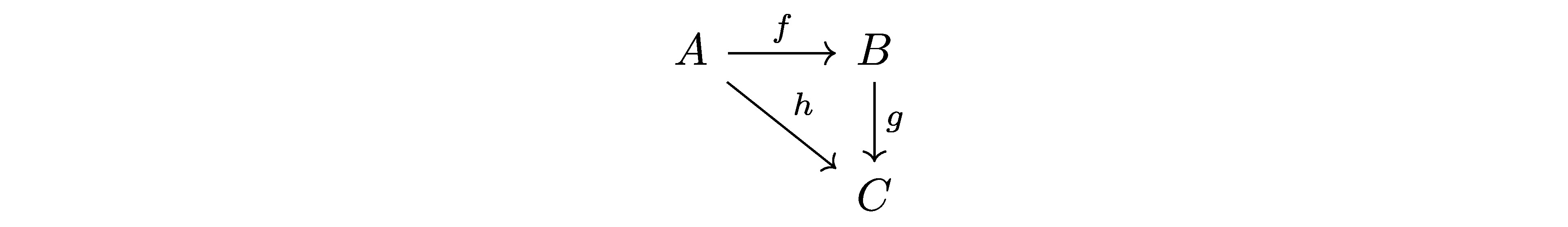等式$h = g \circ f$必须成立。

从Product开始的范畴论语义

范畴语义是什么

于是我们得到了范畴的定义。这很好，但这很数学。这和编程语言、和STLC有什么关系呢？要回答这个问题，我们首先需要知道对于一门编程语言来说，语义是什么？一般来说，我们认为编程语言的语义就是这门语言是如何被执行的。但是，这只是语义中的一种：Operation Semantic（操作语义？）。操作语义就是通过一系列规则描述语言中的表达式如何一步步求值，也就是用逻辑规则“实现”了一个解释器来对表达式求值。然而，在编程语言的研究中，还有另外一种很重要的语义描述方式： Denotation Semantic（指称语义？）。指称语义中，我们并不描述表达式是如何求值的，而是将表达式、类型等等在某种数学模型下赋予意义。换言之，指称语义把语言中的表达式“编译”成了数学模型中的对象。那么，这有什么意义呢？我们把C编译成汇编，是因为汇编更容易在机器上执行。而我们通过指称语义把语言编译成数学对象，是因为通过已经被详细研究过的已知数学对象，可以更好地研究语言的性质。

于是，范畴论语义的意义也就非常清晰了：将语言“编译”成某个范畴中的对象、箭头，然后通过对相应的范畴的研究来研究语言本身的结构和性质。但是，范畴论语义又与传统的、基于域论、集合和函数的指称语义有着很大的不同。在基于集合与函数的语义中，目标数学模型本身就有函数这种带有“求值”的感觉的构造，因而这种语义看上去更像一个解释器、一个用集合与函数实现的解释器。但是，范畴中并没有“函数”的概念。虽然我们有箭头，但箭头并没有“接受参数”的功能。所以在以范畴论为模型的指称语义中，很难找到任何“求值”的感觉。那么，这意味着什么呢？在我看来，这意味着范畴论语义并不是关于表达式的求值的，而是对类型系统自身的结构的反映。我们有很多不同的类型系统、不同的逻辑系统，那么它们之间是否有什么相似的结构呢？要回答这一问题，最为方便的工具（之一）就是范畴论语义。

范畴语义的第一步：谁是对象？谁是箭头？

现在，我们终于开始本文的主题了：推导语言的范畴语义。在推导STLC的范畴语义之前，我们应该考虑一个非常重要的问题：我们应该把表达式（此后用meta variable $t$、$u$指代）和类型（此后用meta variable $A$、$B$指代）翻译成范畴中的什么？一个范畴中，无非就是对象和箭头这两类东西。所以我们也应当把表达式和类型翻译成它们。在STLC，以及其他很多类型系统中，类型系统的推导规则的形式是： \[ \Gamma \vdash t : A \] 其中$\Gamma$是记录了变量及其对应类型的上下文。但是，这里出现了一个问题：类型规则中有上下文$\Gamma$、表达式$t$和类型$A$三种东西，但是范畴只有箭头和对象这两种东西。所以上下文、表达式和类型中必须有两样被统一起来。由于上下文中记录的主要是类型，很自然地我们会想把上下文和类型统一起来。那么，该如何做呢？接下来，我们通过把类型也变成上下文来统一它们。这个方法是千里冰封教我的。如果要把类型也看成上下文，那么我们需要克服两个问题：上下文中可以有多个类型，以及上下文中还有变量。对于第二个问题，根据$\alpha$等价，我们知道变量的具体命名其实并不重要。所以我们可以把变量全部按出现为位置命名成$\$i$，把$\Gamma$看成一串类型，或者说只有变量名字的选取不同的所有上下文的等价类。对于第一个问题，如果我们同时引入很多个表达式，我们就可以得到很多个类型了。所以，沿着这种思路，我们得到的解决方案是：把表达式替换成Substitution（用$\sigma$指代）（因为替换/代换这些翻译在本文的语境下太容易出歧义，我就直接用substitution了）。为什么？假如我们有一个substitution $\sigma = [\$1 := t_1, \$2 := t_2, ...]$，那么$\sigma$的类型应该是什么呢？为了描述$\sigma$的类型，我们应该描述出每个$\$i$的类型，所以$\sigma$的类型应该是 \[ \$1 : \text{typeof}(t_1), \$2 : \text{typeof}(t_2), ... \] 这正是一个上下文！此外，$\sigma$中的表达式$t_i$应当在恰当的上下文中被类型检查，所以$\sigma$的类型也需要在一个上下文中被检查！因此，substitution的类型规则形如： \[ \Gamma \vdash \sigma : \Gamma' \] 现在只剩下两种对象了。从推导规则的形式上，我们很自然地把上下文映射成范畴中的对象，把substitution映射成箭头。那么，箭头的源和目的地应当如何选取呢？这时，我们就应当考虑范畴的定义剩下的需求：箭头的复合。 Substitution本身同样能够复合： \[ \begin{aligned} \sigma &= [\$1 := t_1, \$2 := t_2, ...] \\ \sigma' \circ \sigma &= [\$1 := \sigma'(t_1), \$2 := \sigma'(t_2), ...] \end{aligned} \] 由于$\sigma' \circ \sigma$和$\sigma$作用的变量是一致的，它们的类型应该也是一致的。同时，应用$\sigma' \circ \sigma$产生的表达式包含应用$\sigma'$产生的表达式，所以$\sigma' \circ \sigma$和$\sigma'$应当在同样的上下文中被类型检查。于是我们可以得到如下的类型规则： \[ \begin{aligned} \dfrac{ \Gamma \vdash \sigma' : \Gamma', \qquad \Gamma' \vdash \sigma : \Gamma'' }{ \Gamma \vdash \sigma' \circ \sigma : \Gamma'' } \end{aligned} \] 为了保持箭头方向与类型规则方向一致，我们要求substitution对应的箭头从它被检查的上下文指向它的类型。为了保证substitution复合在源与目的地上的正确性， substitution的箭头的复合是substitution自身的反向复合，即： \[ \sigma' \circ \sigma\text{ (as arrow)} = \sigma \circ \sigma'\text{ (as substitution)} \] 最后，单位箭头就是把所有变量替换成它自身的trivial substitution。如此一来，我们就得到了把语言和类型系统中的构造翻译成范畴中的对象和箭头的方法。接下来，我们需要考虑的问题就是：语言对应的范畴应该有怎样的性质和结构？

推导范畴中的乘积定义

在开始讨论$\lambda$之前，我们还缺了重要的一环：上下文，也就是范畴语义中的对象，是由多个类型构成的。我们要如何刻画它的组成？

答案蕴藏在上面统一上下文和类型的过程中。我们把类型看成了上下文，但如果我们要反过来把上下文看成类型的话，应该如何做呢？答案是反向的柯里化：把上下文看成一个大tuple。在自然演绎的上下文/Sequent Calculus的左侧sequence中， “逗号”就是product type的另一种写法罢了。所以，问题就转化成了：我们要如何在范畴中表达两个对象的product/pair？

于是你翻开了一本范畴论教材，找到了product的定义：

在一个范畴$\mathcal{C}$中，对象$A \times B$是两个对象$A$和$B$的product，当且仅当以下条件满足：

有两个箭头$\pi_1 : A \times B \rightarrow A$与$\pi_2 : A \times B \rightarrow B$

对于范畴中的任意对象$C$，如果有两个箭头$f : C \rightarrow A$、$g : C \rightarrow B$，那么存在从$C$到$A \times B$存在一个唯一的箭头$(f,g)$，且：

$\pi_1 \circ (f,g) = f$

$\pi_2 \circ (f,g) = g$

你懂吗？我清楚地记得我在某个晚上初次读到这个定义时受到的震撼：原来区区Cartesian Product也可以定义成人类难以理解的样子。但没有关系，虽然范畴论教材不太靠得住，我们已经知道了类型系统与范畴之间是有一定联系的，而我们也知道在STLC中的product type相关的规则是怎样的： \[ \dfrac{\Gamma \vdash t : A, \quad \Gamma \vdash u : B}{\Gamma \vdash (t, u) : A \times B} \qquad \dfrac{\Gamma \vdash t : A \times B}{\Gamma \vdash \text{fst}(t) : A} \qquad \dfrac{\Gamma \vdash t : A \times B}{\Gamma \vdash \text{snd}(t) : B} \] 还记得我们是如何把类型规则变成范畴中的结构的吗？运用上面的对应，我们可以把这些类型规则翻译成范畴中的交换图：如果我们把范畴中product的定义的交换图也画出来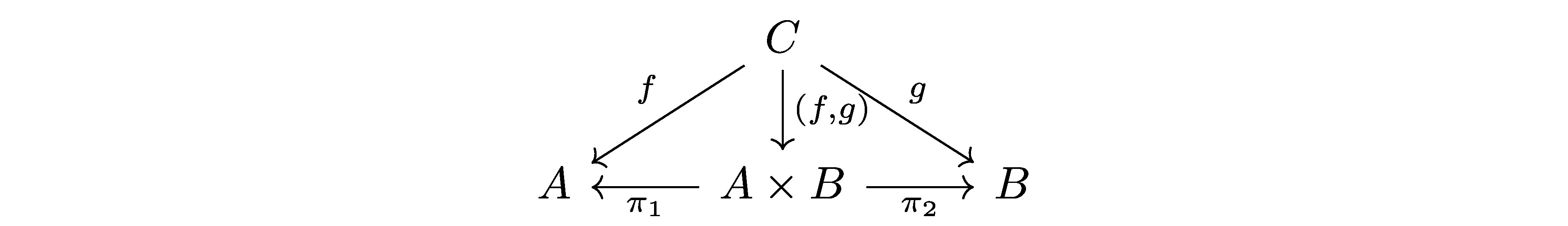：可以看到，这两种交换图之间似乎非常相似但又不完全相同。首先观察到，$(t,u)$与$(f,g)$无疑是高度相似的。在编程语言的一侧，只要我们有$t$、$u$两个表达式，就能写出它们的组合$(t,u)$，$(t,u)$的类型是$t$和$u$类型的product。而在范畴一侧，给定任意的$f$、$g$两个箭头，我们也能得到一个箭头$(f,g)$指向$f$、$g$目的地的product。显然，这两者是一致的。但接下来，类型规则产生的交换图中缺少了两个箭头：$\pi_1$和$\pi_2$。同时多了两个箭头$\text{fst}(t)$和$\text{snd}(u)$。一个很自然的猜想自然是： \[ \begin{aligned} \text{fst}(t) &= \pi_1 \circ t \\ \text{snd}(t) &= \pi_2 \circ t \end{aligned} \] 于是我们得到了$\pi_1$和$\pi_2$在语言中的构造： $\pi_1 = \text{fst}(\$1)$，$\pi_2 = \text{snd}(\$1)$。现在我们已经统一了编程语言中的product和范畴论的product的大部分性质，只剩下最后一条： \[ \begin{aligned} \pi_1 \circ (f,g) &= f \\ \pi_2 \circ (f,g) &= g \end{aligned} \] 把上面的对应代进去，这两条等式在编程语言语境下就变成了： \[ \begin{aligned} \text{fst}((t, u)) &= t \\ \text{snd}((t, u)) &= u \end{aligned} \] 所以范畴论的定义和类型系统的定义是完全一致的！现在，用编程语言的视点再次审视范畴中product的定义，是否觉得它看上去更加自然了？于是现在我们解决了product如何在范畴中定义的问题。现在，我们可以把复合的上下文定义成一系列类型的乘积。并且，我们可以给STLC的范畴模型加上第一条性质了：

STLC的范畴模型中，必须存在finite product。也就是，给定范畴中的有限个对象，它们的乘积必须也存在于范畴中

为什么乘积存在还需要说明？如果你再仔细读一读范畴中乘积的定义，它只是描述了一个乘积应该是什么样的，却没有说它一定存在。如果你把文章开头范畴的定义找出来，很容易看出那几条简单得定义显然并不足以证明任意对象的乘积存在。这说明并不是随便哪个范畴都可以用来描述STLC的语义。如果我们要用一个范畴来描述STLC的语义，它的任意两个对象的乘积必须也存在与这个范畴之中。

此后，为了记号的简洁，我们定义乘积上的一个额外的操作符： \[ \begin{aligned} &f : A \rightarrow C \\ &g : B \rightarrow D \\ &f \times g : A \times B \rightarrow C \times D = (f \circ \pi_1, g \circ \pi_2) \end{aligned} \] 直觉上看，$f \times g$分别将$f$和$g$用于映射一个pair中的两个分量，得到一个新的pair。

Terminal Object

我们已经找到了范畴语义中对象和箭头的对应，也通过product知道了复合的上下文如何构建。不过，还有一个不起眼却重要的存在被遗漏了：空的上下文应该如何表达？如果我们继续通过一个大tuple来理解上下文，那么空的上下文就是一个空的tuple。但我们现在拥有的只有二元的product定义。所以我们还需要在范畴中另找一个对象来表示空的tuple。

为了在范畴中构造出空的tuple，我们需要知道它拥有的性质。范畴中的二元product是满足结合律的（证明留作练习），因此我们可以把一个范畴中的n-tuple看成一个列表，那么“$\times$”就是拼接列表的操作，而空的tuple就是空的列表。如果你还记得文章开头的幺半群的定义的话，列表与拼接列表的操作构成一个幺半群，而空列表就是它的单位元。所以，空tuple的性质就是： \[ \forall A, \quad A \times () = () \times A = A \] 因此，如果把这条性质编码进范畴中，我们就能在范畴中构造出空的tuple了。

为了了解$A = A \times ()$会带来什么性质，我们不妨将$A$代入范畴乘积的交换图中：为了证明$A = A \times ()$，我们需要：

构造出$(f,g)$、$\pi_1$和$\pi_2$
证明$\pi_1 \circ (f,g) = f$，$\pi_2 \circ (f,g) = g$

$(f,g)$和$\pi_1$的构造是十分显然的：分别取$f$和$\text{id}_A$即可。那么，$\pi_2$应该如何构造呢？这里就是$()$的性质该上场的地方了。事实上，有一条十分简洁的定义可以满足我们的全部要求：

对于范畴中的任意对象$B$，存在唯一的从$B$指向$()$的箭头，记作$!_B$

这条定义首先给了我们一个唯一的$\pi_2$的构造方式：$\pi_2 =\ !_A$。此外，由于从$C$到$()$的箭头同样只能是$!_C$，而$!_A \circ f = \pi_2 \circ (f,g)$同样是一个从$C$到$()$的箭头，我们又得到了：$\pi_2 \circ (f,g) =\ !_C = g$。因此，上面对$()$的定义是可以满足我们的要求的。事实上，像上面这样定义出的$()$是范畴论中一种十分重要的构造，叫作terminal object。

于是现在我们得到了关于STLC的范畴模型的第二条性质：

STLC的范畴模型中必须存在terminal object

事实上，如果把terminal object看作0个元素的tuple，这一条性质也可以包含在前一条“finite product存在”的性质中。现在，关于上下文的一切已经定义完毕。我们也可以终于向本文的主角：$\lambda$发起挑战了。但在此之前，在获得了terminal object的定义之后，我想展示关于范畴乘积的另一种定义。在介绍范畴语义时我宣称“范畴可以帮助我们更好地研究类型系统的性质”，而现在，我将用一个例子展示这是如何做到的。

在介绍范畴乘积的第二种定义之前，首先我们需要一个新的定义：subcategory（子范畴）。对于一个范畴$\mathcal{C}$，它的子范畴$\mathcal{D}$是一个满足如下条件的范畴：

$\mathcal{D}$中的对象是$\mathcal{C}$中的对象的子集。
如果有箭头$f \in \mathcal{D}(A, B)$，那么$f \in \mathcal{C}(A, B)$。即$\mathcal{D}$中的箭头也是$\mathcal{C}$中箭头的子集，且箭头的源和目的地在$\mathcal{C}$、$\mathcal{D}$中相同。
$\mathcal{D}$中的箭头复合就是$\mathcal{C}$中的箭头复合， $\mathcal{D}$中的单位箭头就是$\mathcal{C}$中的单位箭头。

如果我们加上一条额外的条件：

如果$A, B \in \mathcal{D}$，$f \in \mathcal{C}(A,B)$，那么$f \in \mathcal{D}(A, B)$

那么这是$\mathcal{D}$就称为$\mathcal{C}$的一个full subcategory（不会译）。这条条件说的是，如果两个对象$A$、$B$都在$\mathcal{D}$中， $\mathcal{D}$不会丢弃任何一个$A$、$B$间的箭头。

那么这个定义有什么意义呢？ Full subcategory这一定义的一种直观解释是：我们只关心$\mathcal{C}$中的特定的某些对象，因此我们把不关心的对象全部移除，得到一个更小的范畴，从而使我们能够更好地研究我们关心的那些对象与它们之间的关系。

有了full subcategory的定义之后，我们就可以用它来定义范畴乘积了：

在范畴$\mathcal{C}$中，取所有满足下列交换图的对象$C$构成一个$\mathcal{C}$的full subcategory $\mathcal{C}'$： \[ A \longleftarrow C \longrightarrow B \] 那么$A$、$B$的乘积$A \times B$就是这个subcategory中的terminal object。

通过纯范畴论的推理，很容易证明这一定义与上面的范畴乘积定义是等价的。但是这里更为重要的是这个定义在范畴之外的意义。如果我们把上面这个定义用STLC、自然演绎的视点来看会怎么样呢？这里由于表达式的存在不是非常重要，我们并不直接讨论STLC中的类型规则，而是讨论抹除了表达式得到的逻辑系统、自然演绎的规则。在最开始的定义中，从STLC的视点看，乘积定义其实说了三件事：

乘积的introduction
乘积的elimination
乘积的introduction和elimination之间的关系

那么这个新的定义又传达了什么信息呢？我们知道$A \times B$首先必须在subcategory $\mathcal{C}'$中，所以必须有两个箭头$\pi_1 : A \times B \rightarrow A$与$\pi_2 : A \times B \rightarrow B$。这一点与前一个定义一致，描述了乘积的elimination。但是introduction去哪了？我们只有$A \times B$是$\mathcal{C}'$中的terminal object这一信息。这就是说，从$\mathcal{C}'$中的任意对象$\Gamma$，有一个唯一的箭头$!_{\Gamma} : \Gamma \rightarrow A \times B$。如果把这个信息用逻辑规则写出： \[ \Gamma \vdash A \times B \] 它说的其实是$\Gamma$能够推出$A \times B$。

于是我们可以得到这个新的乘积定义在逻辑系统中的含义：

只要某个上下文$\Gamma$能够像$A \times B$一样被使用，也就是它能够像$A \times B$一样被eliminate，那么它就比$A \times B$更强、能够推出$A \times B$ 所以$A \times B$是满足其elimination rule的所有命题里最弱的一个。

从这个新的乘积定义里，我们得到了从逻辑规则的形式中并不那么显然的新信息！如果你看STLC/自然演绎中乘积的introduction和elimination： \[ \dfrac{\Gamma \vdash A, \quad \Gamma \vdash B}{\Gamma \vdash A \times B} \qquad \dfrac{\Gamma \vdash A \times B}{\Gamma \vdash A} \qquad \dfrac{\Gamma \vdash A \times B}{\Gamma \vdash B} \] 就能发现这条隐藏的、introduction条件和elimination之间的关系！在逻辑系统中，对于一个构造的introduction和elimination必须满足 local reduction和local expansion这两条性质，它们说的是：

introduction之后再elimination应该能得到原来的条件，也就是说introduction的条件不能过强
elimination之后再introduction应该能得到原来的命题，也就是说elimination的结论不能过弱

而采用新定义的乘积的范畴语义告诉我们的，不正是这一点吗？它告诉我们的，正是introduction和elimination的强弱是精确匹配的。

所以，通过范畴语义，我们“发现”了STLC/自然演绎中，乘积的introduction和elimination在形式上的联系，而这一条形式上的相似性对应的恰恰是至关重要的local reduction/expansion性质。所以，范畴语义的确能够帮助我们发现规则的语法背后的、系统的深层结构与性质。

lambda, finally

在经过漫长的铺垫后，我们终于可以面对本文的主角：$\lambda$了。但其实在经过前面的推导之后，$\lambda$的范畴语义的推导并没有什么难的，只不过是把上面的过程重复一遍罢了。为了得到$\lambda$的语义，我们只需要把它的类型规则写出，将这些规则翻译成范畴，并用范畴的语言表述即可。首先考察STLC中$\lambda$的类型规则： \[ \dfrac{\Gamma, x : A \vdash t : B}{\Gamma \vdash \lambda x.t : A \rightarrow B} \qquad \dfrac{ \Gamma \vdash t : A \rightarrow B, \quad \Gamma \vdash u : A }{ \Gamma \vdash \text{app}(t,u) : B } \] 我们可以把这些规则直接翻译成范畴语言：其中$[\![ A \rightarrow B ]\!]$是函数类型$A \rightarrow B$的范畴构造，我们暂时还不知道它是什么。此外，我们还有$\beta$ reduction： \[ \text{app}(\lambda x.t, u) = t[x := u] = t \circ u \] 根据这些图与等式，我们已经可以得到$\lambda$在范畴中的一个定义了：

在范畴$\mathcal{C}$中，$[\![ A \rightarrow B ]\!]$是一个满足如下条件的对象：

对于任意的箭头$t : \Gamma \times A \rightarrow B$，存在一个唯一的箭头$\lambda t : \Gamma \rightarrow [\![ A \rightarrow B ]\!]$

对于任意的箭头$t : \Gamma \rightarrow [\![ A \rightarrow B ]\!]$ 与$u : \Gamma \rightarrow A$，存在一个箭头$\text{app}(t, u) : \Gamma \rightarrow B$

对于任意的$t : \Gamma \times A \rightarrow B$与$u : \Gamma \rightarrow A$， $\text{app}(\lambda t, u) = t \circ (\text{id}_\Gamma, u)$

不过，这个定义似乎还是有些复杂。在范畴的乘积定义中，我们把$\text{fst}(t)$和$\text{snd}(t)$用$\pi_1 \circ t$和$\pi_2 \circ t$代替了。这样我们就不需要定义一大家族的箭头$\text{fst}(t)$和$\text{snd}(t)$，而只需要定义两个箭头$\pi_1$和$\pi_2$了。那么，这里我们是否也可以运用类似的技巧呢？这里$\text{app}(t, u)$有两个参数，所以我们可以把对应$\text{app}$的箭头如此定义： \[ \text{app} : [\![ A \rightarrow B ]\!] \times A \rightarrow B \] $\beta$ reduction的性质则可以定义为： \[ \text{app} \circ (\lambda t, u) = t \circ (\text{id}_\Gamma, u) \] 现在，我们已经可以把这个定义整理到一张交换图里了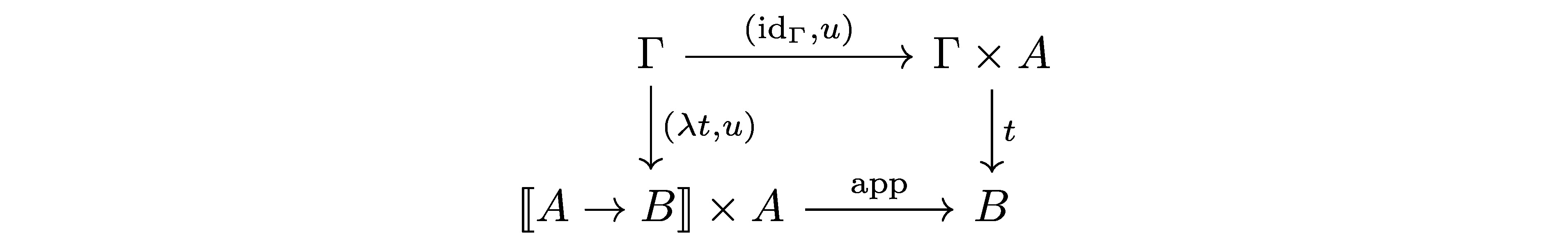：不过我们能做的还有更多。我们想像乘积时那样，从范畴模型中找到local reduction/expansion，找到$\lambda$的introduction和elimination之间的联系。再次把introduction与elimination的规则用交换图写出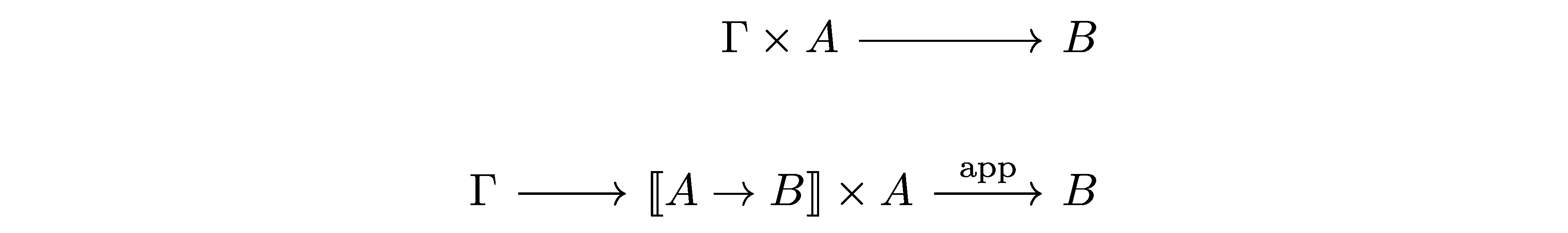：观察到惊人的相似性了吗？如果我们把$\lambda$的elimination $[\![ A \rightarrow B ]\!] \times A \rightarrow B$ 的形式，那么$\lambda$的introduction中的条件有着完全相同的形式！所以我们可以给出$\lambda$在范畴语义中的terminal object定义：

取范畴$\mathcal{C}$中所有满足下列交换图的对象$\Gamma$构成一个full subcategory $\mathcal{C}'$： \[ \Gamma \times A \longrightarrow B \] 那么$[\![ A \rightarrow B ]\!]$就是subcategory $\mathcal{C}'$中的terminal object

读者可以自行（通过纯范畴论的推理）证明这一定义和刚刚那个是等价的。和乘积时一样，这个定义告诉我们$\lambda$的introduction与elimination的强度是匹配的。从这个定义中，我们能够得到一张进一步简化的交换图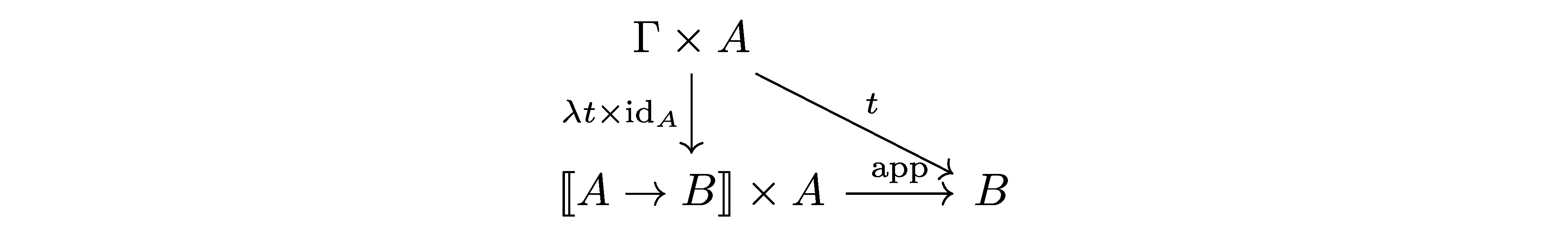：事实上，范畴论中“刚好”有一个构造和这张交换图一模一样，它叫做exponential，记作$B^A$。我们的箭头$\text{app}$被叫做$\text{eval}$，而$\lambda t$的名字还是$\lambda t$ （这些命名使我怀疑exponential就是因为和STLC的联系才被发现的，但我没有证据）。并且现在我们能够将STLC的范畴论模型应当具备的所有性质写出来了：

STLC的范畴论模型应当满足以下三条性质：

存在terminal object

存在finite product

存在任意两个对象的exponential

如果你去找一种叫做“Cartesian Closed Category”的东西，你会找到一个完全相同的定义。所以，是的，我们找到了STLC的标准范畴论模型。接下来我们就可以通过研究Cartesian Closed Category来研究STLC的类型规则背后的结构与性质了。例如，在范畴论中，exponential之所以叫这个名字，其原因之一是它满足如下等式： \[ \left(C^B\right)^A = C^{A \times B} \] 如果我们把这条等式翻译成STLC会得到： \[ A \rightarrow (B \rightarrow C) = A \times B \rightarrow C \] 这不正是我们熟悉的柯里化吗？又比如，在STLC中有著名的$\eta$ expansion $\lambda x. f\ x = f$，如果我们把相关的元素翻译成交换图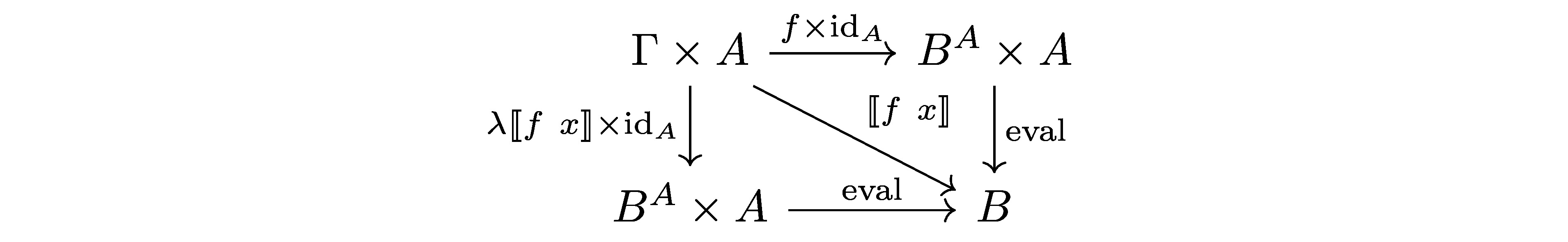：其中$[\![ f\ x ]\!] = \text{eval} \circ (f \times \text{id}_A)$是$f\ x$在范畴语义中的构造。这里我们有$f, \lambda [\![ f\ x ]\!] : \Gamma \rightarrow B^A$，但是$B^A$是一个terminal object！所以$f = \lambda [\![ f\ x ]\!]$， $\lambda t$的唯一性就是$\eta$ expansion！